Составим логическую цепь трехвходовой пороговой

2.7. Синтез пороговой ячейки

Пороговая ячейка. Составим логическую цепь трехвходовой пороговой ячейки, сигнал на выходе которой будет равен 1; когда на ее входах присутствует не менее двух единиц.

1. Составим таблицу функционирования.

	X1	X2	X3	F
1	0	0	0	0
2	0	0	1	0
3	0	1	0	0
4	0	1	1	1
5	1	0	0	0
6	1	0	1	1
7	1	1	0	1
8	1	1	1	1

2. Для составления логической функции необходимо составить сумму конъюнкций (произведений) всех логических переменных, соответствующих тем строкам, где логическая функция равна 1, причем в конъюнкциях переменная берется без инверсии, если она равна 1, и с инверсией в противном случае:

3. Минимизация полученного выражения. Применим для членов 3 и 4 закон склеивания.

Умножим последнее слагаемое на (1+Х3) (это не изменит общее выражение) и повторим предыдущую процедуру.

Вновь умножим третье слагаемое на (1+Х3):

Применим для слагаемых 3 и 4 закон поглощения. Получим

- это и есть минимизированная функция.

4. Приведем функцию к виду, удобному для реализации на элементах И-НЕ:

.

Применим правило Моргана: Y =

Это выражение можно реализовать в базисе И-НЕ.

Исходя из полученного выражения составим схему (рис.2.19)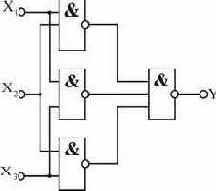

Рис. 2.19. Схема пороговой ячейки

Содержание раздела

Главная сайта